Question
The correct statement (s) about the compund given below is (are)

Found 4 tutors discussing this question
Discuss this question LIVE
10 mins ago
Filo tutor solution
Learn from their 1-to-1 discussion with Filo tutors.
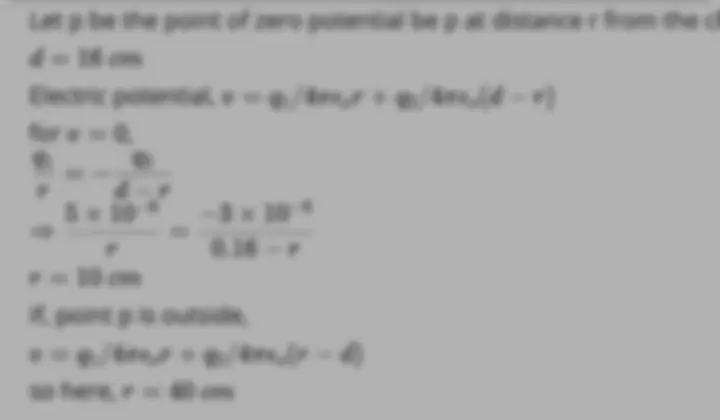
Generate FREE solution for this question from our expert tutors in next 60 seconds
Don't let anything interrupt your homework or exam prep with world’s only instant-tutoring, available 24x7
Practice questions from similar books
Question 4
Let , be the number of red and black balls, respectively, in box I. Let ,be the number one red and b of red and black balls, respectively, in box II. A ball is drawn at random from box 1 and transferred to box II. If the probability of drawing a red ball from box I, after this transfer, is then the correct option(s) with the possible values of , is(are) | Question Text | The correct statement (s) about the compund given below is (are) |



